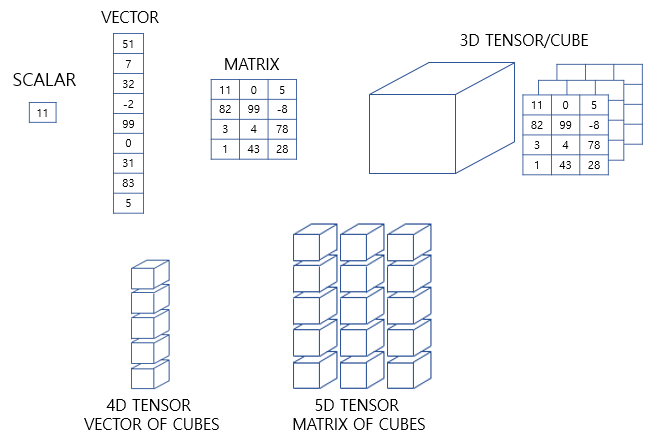
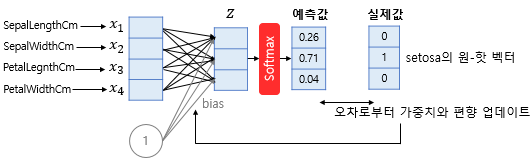
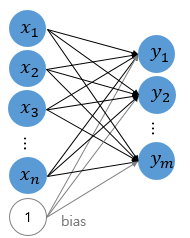
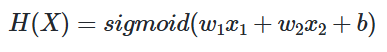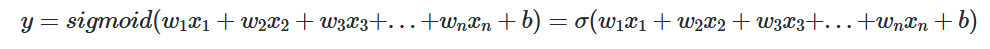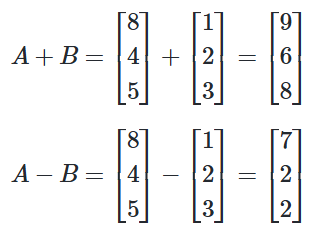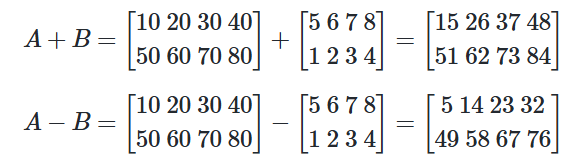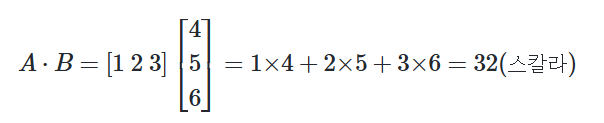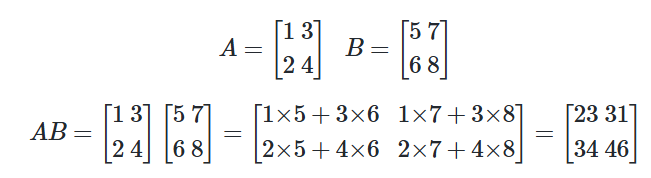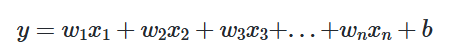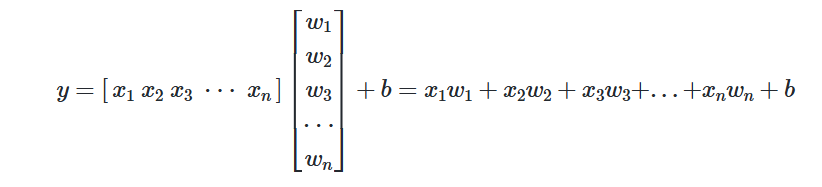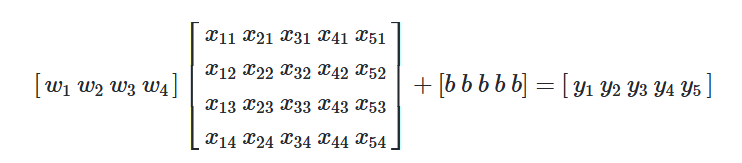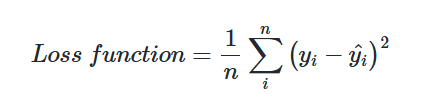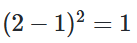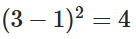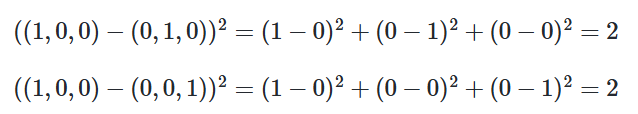가장 많이 쓰이고 중요한 케라스 함수를 정리했습니다.
📝Tokenizer
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
tokenizer = Tokenizer()
train_text = "The earth is an awesome place live"
# 단어 집합 생성
tokenizer.fit_on_texts([train_text])
# 정수 인코딩
sub_text = "The earth is an great place live"
sequences = tokenizer.texts_to_sequences([sub_text])[0]
print("정수 인코딩 : ",sequences)
print("단어 집합 : ",tokenizer.word_index)
# 정수 인코딩 : [1, 2, 3, 4, 6, 7]
# 단어 집합 : {'the': 1, 'earth': 2, 'is': 3, 'an': 4, 'awesome': 5, 'place': 6, 'live': 7}전처리 과정에 사용 되며 문장을 토큰으로 나누고 정수 인코딩에 사용 됩니다.
pad_sequences([[1, 2, 3], [3, 4, 5, 6], [7, 8]], maxlen=3, padding='pre')- pad_sequence()
- 각 샘플의 길이가 서로 다를 수 있는데 모델에 입력할 때 모든 샘플의 길이를 동일하게 맞춰야 할 때가 있습니다. 이걸 패딩이라고 하는데 부족한 곳에는 0을 채워넣고 너무 과한 곳은 아예 잘라버립니다.
📝층 입력하기
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
# 워드 임베딩
model.add(Embedding(vocab_size, output_dim, input_length))
# 전결합층 추가
model.add(Dense(1, input_dim=3, activation='relu'))- Sequential()
- 층을 만들기 위한 작업입니다.
- Embedding
- 첫번째 인자 → 단어의 잡합의크기로 총 단어의 개수를 의미합니다.
- 두번째 인자 → 임베딩 벡터의 출력 차원 (대체로 상황에 쓰이는 추천 출력 차원 존재) [너무 작으면 의미가 사라지며 크면 커지고 과적합 위험]
- 세번째 인자 → 입력 시퀀스 길이 (문장안에 몇 단어로 들어가는지로 정하게 되며 길이가 부족한 건 패딩처럼 처리가 된다)
- Dense
- 첫번째 인자 → 출력 뉴런 수
- input_dim → 입력 뉴런 수
- activation → 활성화 함수
📝모델 정보 요약
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 8) 40
_________________________________________________________________
dense_2 (Dense) (None, 1) 9
=================================================================
Total params: 49
Trainable params: 49
Non-trainable params: 0
_________________________________________________________________
📝컴파일
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])- compile
- 모델을 기계가 이해할 수 있게 컴파일 합니다.
- optmizer → 훈련 과정을 설정하는 옵티마이저 설정
- loss → 훈련 과정에 사용할 손실 함수 설정
- metrics → 훈련을 모니터링하기 위한 지표를 선택
| 문제 유형 | 손실 함수명 | 출력층의 활성화 함수명 | 참고 실습 |
| 회귀 문제 | mean_squared_error | - | 선형 회귀 실습 |
| 다중 클래스 분류 | categorical_crossentropy | 소프트맥스 | 로이터 뉴스 분류하기 |
| 다중 클래스 분류 | sparse_categorical_crossentropy | 소프트맥스 | 양방향 LSTM를 이용한 품사 태깅 |
| 이진 분류 | binary_crossentropy | 시그모이드 | IMDB 리뷰 감성 분류하기 |
📝훈련
model.fit(X_train, y_train, epochs=10, batch_size=32)
model.fit(X_train, y_train, epochs=10, batch_size=32, verbose=0, validation_data(X_val, y_val))
# 훈련 데이터의 20%를 검증 데이터로 사용.
model.fit(X_train, y_train, epochs=10, batch_size=32, verbose=0, validation_split=0.2))- fit
- 모델을 학습합니다.
- 첫번째 인자 → 훈련 데이터에 해당
- 두번째 인자 → 지도 학습에서 레이블 데이터에 해당
- epochs → 에포크로 1은 전체 데이터를 한 차례 훑고 지나갔음을 의미. 총 훈련 횟수를 정의
- batch_size → 배치 크기로 기본값은 32입니다. 미니 배치 경사 하강법을 사용하고 싶지 않을 경우 batch_size=None
- verbose → 학습 중 출력 문구를 설정 (0 → 출력 X, 1 → 훈련 진행에 대한 막대, 2 → 미니 배치마다 손실 정보 출력)
- validation_data(x_val, y_val) → 검증 데이터를 사용합니다. 각 에포크 마다 검증 데이터의 정확도나 오차를 출력하는데 이건 훈련이 잘 되고 있는지를 보여줄 뿐이지 이 데이터를 학습하진 않습니다. (과적합에 대한 판단 가능)
- validation_split → 훈련 데이터와 훈련 데이터의 레이블인 x_train, y_train에서 일정 비율 분리해 검증 데이터로 사용
📝평가
# 위의 fit() 코드의 연장선상인 코드
model.evaluate(X_test, y_test, batch_size=32)- evaluate
- 테스트 데이터를 통해 학습한 모델에 대한 정확도를 평가합니다.
- 첫번째 인자 → 테스트 데이터에 해당
- 두번째 인자 → 지도 학습에서 레이블 테스트 데이터에 해당
- batch_size → 배치 크기
📝예측
# 위의 fit() 코드의 연장선상인 코드
model.predict(X_input, batch_size=32)- predict
- 임의의 입력에 대한 모델의 출력값을 확인합니다.
- 첫번째 인자 → 예측하고자 하는 데이터
- batch_size → 배치 크기
📝모델 저장과 로드
model.save("model_name.h5")
from tensorflow.keras.models import load_model
model = load_model("model_name.h5")- save
- 인경 신경망 모델을 hdf5 파일에 저장
- load_model
- 저장해둔 모델을 불러옵니다.
🔗 참고 및 출처