📝선형회귀

시험 공부하는 시간을 늘리면 늘릴 수록 성적이 잘 나옵니다. 하루에 걷는 횟수를 늘릴 수록, 몸무게는 줄어듭니다. 집의 평수가 클수록, 집의 매매 가격은 비싼 경향이 있습니다. 이는 수학적으로 생각해보면 어떤 요인의 수치에 따라서 특정 요인의 수치가 영향을 받고있다고 말할 수 있습니다. 수학적인 표현을 써보면 어떤 변수의 값에 따라서 특정 변수의 값이 영향을 받고 있다고 볼 수 있습니다.
즉, 핵심은 어떤 데이터들로부터 상관관계를 함수로 표현하고 그 함수에 해당하는 가중치와 절편 값을 찾아가는 과정입니다. 그러면 어떠한 모르는 값이 들어가도 함수로 유추할 수 있죠
📝단순 선형회귀

단순 선형회귀의 경우 하나의 변수만 있는 경우를 의미합니다. 예를 들면 몸무게에 따른 키로 봤을 때 몸무게가 x값이 되는 거고 그에 따른 통계를 냈을 때 몸무게에 대한 영향은 w(가중치)를 갖게 됩니다. 절편의 값은 그에 따른 조정이 필요할 때 추가적으로 들어가게 됩니다.
즉, 독립 변수 x와 곱해지는 값 w를 머신 러닝에서는 가중치(weight), 별도로 더해지는 값 b를 편향(bias)이라고 합니다.
📝다중 선형회귀

집의 매매 가격은 단순히 집의 평수가 크다고 결정되는 게 아니라 집의 층의 수, 방의 개수, 지하철 역과의 거리와도 영향이 있습니다. 이러한 다수의 요소를 가지고 집의 매매 가격을 예측해보고 싶습니다. y는 여전히 1개이지만 이제 x는 1개가 아니라 여러 개가 되었습니다. 즉, 다양한 요인들이 포함된 경우를 다중 선형 회귀 분석이라고 합니다.
📝목적함수, 비용함수, 손실함수
결국 w와 b를 잘 찾아내는게 목표입니다. w와 b를 찾기 위해서 실제값과 가설로부터 얻은 예측값의 오차를 계산하는 식을 세우고, 이 식의 값을 최소화하는 최적의 w와 b를 찾아냅니다.
실제값과 예측값에 대한 오차에 대한 식을 목적 함수(Objective function) 또는 비용 함수(Cost function) 또는 손실 함수(Loss function) 라고 합니다.
비용 함수는 단순히 실제값과 예측값에 대한 오차를 표현하면 되는 것이 아니라, 예측값의 오차를 줄이는 일에 최적화 된 식이어야 합니다.
손실함수 = (평균제곱오차)

실제값과 예측값을 비교하는 표가 있는데 오차는 = 실제값 - 예측값으로 모든 오차를 다 더하면 음수 오차도 있고 양수 오차도 있기 때문에 거리를 제곱하고 더한 후에 개수만큼 나눕니다.

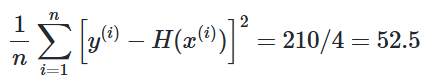
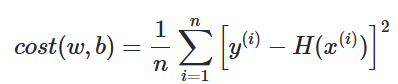
오차가 클수록 평균 제곱 오차는 커지며 작을수록 평균 제곱 오차는 작아집니다.
📝옵티마이저, 경사하강법
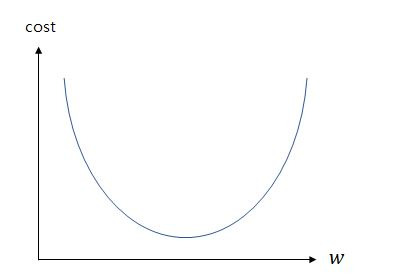
비용 함수를 최소화하기 위해 파라미터 조정하는 과정을 의미합니다. 위 그림은 가중치에 따른 손실함수의 값을 그래프로 만든것인데 cost가 가장 낮은 범위를 찾아야 가장 최적의 조건의 학습이 되는 것입니다. 위 그림을 보면 한눈에 w에따른 cost값을 알수 있지만 전부 다 저렇게 알 수 있지 않습니다.
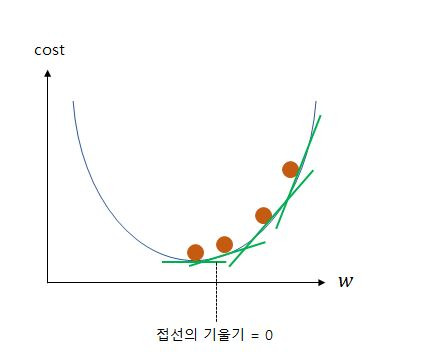
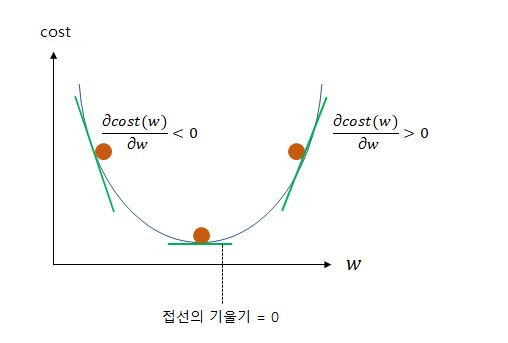
그렇기 때문에 하나하나씩 차근차근 경사 하강법을 이용해 미분해서 기울기 값이 가장 작아지는 경우를 찾아가는 겁니다.
📝선형회귀 실습
import tensorflow as tf
# tf.Variable은 변수에 대한 값을 지정할 때 사용 (가중치와 절편에 값 지정)
w = tf.Variable(4.0)
b = tf.Variable(1.0)
# w*x + b 형태의 선형회귀함수를 가진다.
@tf.function
def hypothesis(x):
return w*x + b
# 손실함수 (제곱오차의 평균)
@tf.function
def mse_loss(y_pred, y):
# 두 개의 차이값을 제곱을 해서 평균을 취한다.
return tf.reduce_mean(tf.square(y_pred - y))
x = [1, 2, 3, 4, 5, 6, 7, 8, 9] # 공부하는 시간
y = [11, 22, 33, 44, 53, 66, 77, 87, 95] # 각 공부하는 시간에 맵핑되는 성적
# 경사 하강법을 이용하며 0.01 정도로 하강하며 적용
optimizer = tf.optimizers.SGD(0.01)
# 300번을 순회하며 처음 설정한 w, b값을 기준으로 선형회귀함수를 가지는 걸 제곱오차로 따져서 경사 하강법을 적용시키며 최적의 cost값을 찾는 과정
for i in range(301):
with tf.GradientTape() as tape:
# 현재 파라미터에 기반한 입력 x에 대한 예측값을 y_pred
y_pred = hypothesis(x)
# 평균 제곱 오차를 계산 (예측값과 실제값 비교)
cost = mse_loss(y_pred, y)
# 손실 함수에 대한 파라미터의 미분값 계산
gradients = tape.gradient(cost, [w, b])
# 경사하강법에 나온 w와 b값을 조정하며 파라미터 업데이트
optimizer.apply_gradients(zip(gradients, [w, b]))
# 10번 루프마다 체크
if i % 10 == 0:
print("epoch : {:3} | w의 값 : {:5.4f} | b의 값 : {:5.4} | cost : {:5.6f}".format(i, w.numpy(), b.numpy(), cost))Tensorflow로 직접 구현하기
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
x = [1, 2, 3, 4, 5, 6, 7, 8, 9] # 공부하는 시간
y = [11, 22, 33, 44, 53, 66, 77, 87, 95] # 각 공부하는 시간에 맵핑되는 성적
model = Sequential()
# 출력 y의 차원은 1. 입력 x의 차원(input_dim)은 1
# 선형 회귀이므로 activation은 'linear'
model.add(Dense(1, input_dim=1, activation='linear'))
# sgd는 경사 하강법을 의미. 학습률(learning rate, lr)은 0.01.
sgd = optimizers.SGD(lr=0.001)
# 손실 함수(Loss function)은 평균제곱오차 mse를 사용합니다.
model.compile(optimizer=sgd, loss='mse', metrics=['mse'])
# 주어진 x와 y데이터에 대해서 오차를 최소화하는 작업을 300번 시도합니다.
model.fit(x, y, epochs=300)
plt.plot(x, model.predict(x), 'b', x, y, 'k.')
plt.show()
# 8.5시간 공부했을 때 성적 예측하기
print(model.predict([9.5]))
# [[89.20797]]Keras로 구현해보기
로직에 대해서 대충 파악하고 이미 잘 만들어진 Keras를 이용하는게 좋긴합니다.
📝이진 분류 (로지스틱 회귀)
둘 중 하나를 결정하는 문제를 이진 분류(Binary Classification)라고 합니다. 그리고 이런 문제를 풀기 위한 대표적인 알고리즘으로 로지스틱 회귀(Logistic Regression)가 있습니다
| score(x) | result(y) |
| 45 | 불합격 |
| 50 | 불합격 |
| 55 | 불합격 |
| 60 | 합격 |
| 65 | 합격 |
| 70 | 합격 |
위 데이터에서 합격을 1, 불합격을 0이라고 하였을 때 그래프를 그려보면 아래와 같습니다.
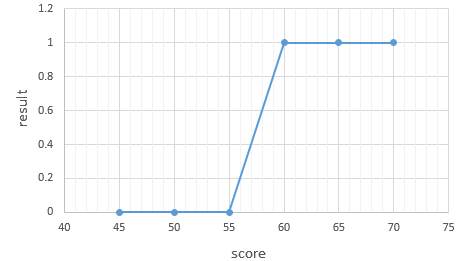
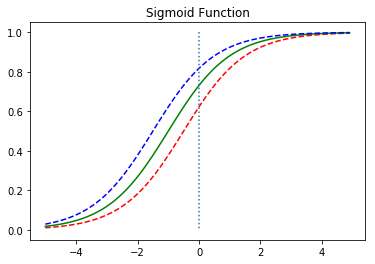
그래프는 알파벳의 S자 형태로 표현됩니다. 이러한 x와 y의 관계를 표현하기 위해서는 직선을 표현하는 함수가 아니라 S자 형태로 표현할 수 있는 함수가 필요합니다.
레이블에 해당하는 y가 0 또는 1이라는 두 가지 값만을 가지므로, 이 문제를 풀기 위해서 예측값은 0과 1사이의 값을 가지도록 합니다. 0과 1사이의 값을 확률로 해석하면 문제를 풀기가 훨씬 용이해집니다. 최종 예측값이 0.5보다 작으면 0으로 예측했다고 판단하고, 0.5보다 크면 1로 예측했다고 판단합니다.
출력이 0과 1사이의 값을 가지면서 S자 형태로 그려지는 함수로 시그모이드 함수(Sigmoid function)가 있습니다.
📝시그모이드 함수(Sigmoid function)
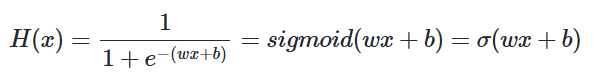
시그모이드 함수는 종종 σ로 축약해서 표현하기도 합니다. 해당 함수는 위와 같이 함수를 표현하는 함수인 것이고 인공지능이 찾아야할 건 결국 w와 b입니다.
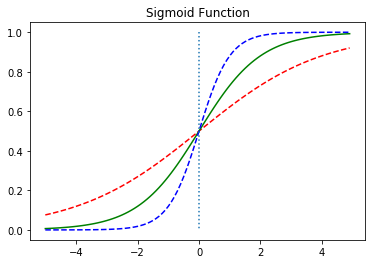
📝로지스틱 손실함수(크로스 엔트로피함수)
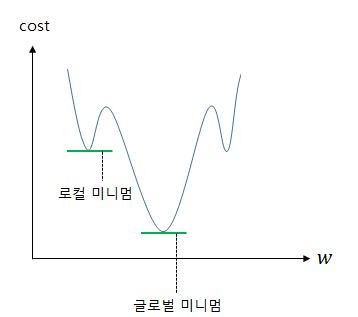
로지스틱 회귀에서 평균 제곱 오차를 비용 함수로 사용하면, 경사 하강법을 사용하였을때 찾고자 하는 최소값이 아닌 잘못된 최소값에 빠질 가능성이 매우 높습니다. 이를 전체 함수에 걸쳐 최소값인 글로벌 미니멈(Global Minimum) 이 아닌 특정 구역에서의 최소값인 로컬 미니멈(Local Minimum) 에 도달했다고 합니다. 로컬 미니멈에 지나치게 쉽게 빠지는 비용 함수는 cost가 가능한한 최소가 되는 가중치 w를 찾는다는 목적에는 좋지 않은 선택입니니다. 그리고 로지스틱 회귀에서의 평균 제곱 오차는 바로 그 좋지 않은 선택에 해당합니다.
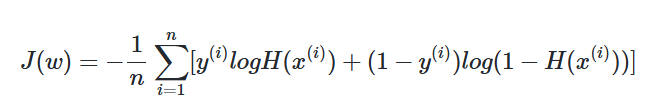
여러가지 계산을 거쳐서 나온 손실함수인데 그 과정을 완전히 무에서 유추하는 거는 솔직히 의미없는 것 같습니다. (사실 안 해봐서 잘 모름) 로지스틱 회귀에서 찾아낸 비용 함수를 크로스 엔트로피(Cross Entropy)함수라고 합니다.
결국엔 아래와 같은 과정을 통해서 진행되게 됩니다.
- 테스트 데이터가 주어진다. (문제와 정답)
- 데이터 결과에 가까운 함수를 사용한다.
- 학습을 시키며 손실함수로 오차범위를 수정하며 해당 함수의 w와 b값을 구한다
- 최적의 w와 b를 이용해 예측이 가능해진다.
🔗 참고 및 출처