📝2개 이상 변수 이중 선형 회귀
딥러닝 챕터로 들어가게되면 대부분의 입력들은 독립 변수가 2개 이상입니다.
| Midterm(x1) | Final(x2) | Added point(x3) | Score($1000)(y) |
| 70 | 85 | 11 | 73 |
| 71 | 89 | 18 | 82 |
| 50 | 80 | 20 | 72 |
| 99 | 20 | 10 | 57 |
| 50 | 10 | 10 | 34 |
| 20 | 99 | 10 | 58 |
| 40 | 50 | 20 | 56 |

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
# 중간 고사, 기말 고사, 가산점 점수
X = np.array([[70,85,11], [71,89,18], [50,80,20], [99,20,10], [50,10,10]])
y = np.array([73, 82 ,72, 57, 34]) # 최종 성적
model = Sequential()
# 입력 차원 설정 (3으로 변경)
model.add(Dense(1, input_dim=3, activation='linear'))
sgd = optimizers.SGD(learning_rate=0.0001)
model.compile(optimizer=sgd, loss='mse', metrics=['mse'])
model.fit(X, y, epochs=2000)
print(model.predict(X))
X_test = np.array([[20,99,10], [40,50,20]])
print(model.predict(X_test))
📝2개 이상 변수 로지스틱 회귀

y를 결정하는데 있어 독립 변수 x가 2개인 로지스틱 회귀를 풀어봅시다. 꽃받침(Sepal)의 길이와 꽃잎(Petal)의 길이와 해당 꽃이 A인지 B인지가 적혀져 있는 데이터가 있을 때, 새로 조사한 꽃받침의 길이와 꽃잎의 길이로부터 무슨 꽃인지 예측할 수 있는 모델을 만들고자 한다면 이때 독립 변수 x는 2개가 됩니다.
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
X = np.array([[0, 0], [0, 1], [1, 0], [0, 2], [1, 1], [2, 0]])
y = np.array([0, 0, 0, 1, 1, 1])
model = Sequential()
model.add(Dense(1, input_dim=2, activation='sigmoid'))
model.compile(optimizer='sgd', loss='binary_crossentropy', metrics=['binary_accuracy'])
model.fit(X, y, epochs=2000)
print(model.predict(X))
# [
# [0.15245897]
# [0.4477718 ]
# [0.43305928]
# [0.7851759 ]
# [0.7749343 ]
# [0.764351 ]
# ]


다중 로지스틱 회귀를 인공 신경망의 형태로 표현하면 다음과 같습니다. 아직 인공 신경망을 배우지 않았음에도 이렇게 다이어그램으로 표현해보는 이유는 로지스틱 회귀를 일종의 인공 신경망 구조로 해석해도 무방함을 보여주기 위함입니다.
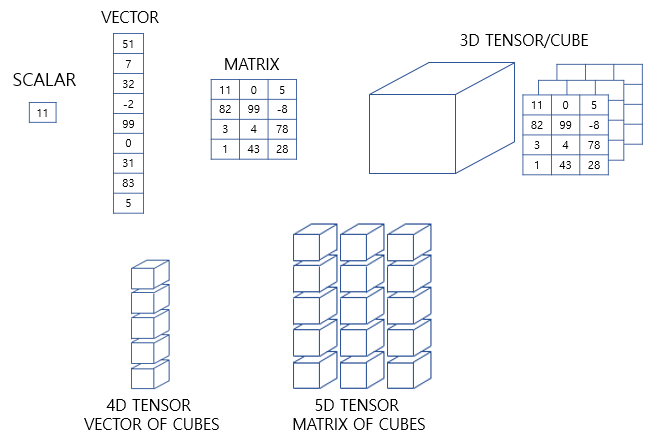
📝텐서, 벡터
1차원은 배열 또는 리스트로 표현합니다. 반면, 행렬은 행과 열을 가지는 2차원 형상을 가진 구조입니다. 파이썬에서는 2차원 배열로 표현합니다. 가로줄을 행(row)라고 하며, 세로줄을 열(column)이라고 합니다. 3차원부터는 주로 텐서라고 부릅니다. 텐서는 파이썬에서는 3차원 이상의 배열로 표현합니다.
0차원 텐서(스칼라)
d = np.array(5)
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)
# 텐서의 차원 : 0
# 텐서의 크기(shape) : ()스칼라는 하나의 실수값으로 이루어진 데이터를 말합니다. 이를 0차원 텐서라고 합니다. 차원을 영어로 Dimension이라고 하므로 0D 텐서라고도 합니다.
1차원 텐서(벡터)
d = np.array([1, 2, 3, 4])
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)
# 텐서의 차원 : 1
# 텐서의 크기(shape) : (4,)벡터는 1차원 텐서입니다. 주의할 점은 벡터에서도 차원이라는 용어를 쓰는데, 벡터의 차원과 텐서의 차원은 다른 개념이라는 점입니다. 위 예제는 4차원 벡터이지만, 1차원 텐서입니다. 1D 텐서라고도 합니다. 참고로 벡터는 1차 텐서에서만 쓰이는 말입니다. → [1,2,3] 일 경우 3차원 벡터이며 x,y,z좌표로 표현한 거라 생각하면 된다.
2차원 텐서(행렬)
# 3행 4열의 행렬
d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)
# 텐서의 차원 : 2
# 텐서의 크기(shape) : (3, 4)행과 열이 존재하는 벡터의 배열. 즉, 행렬(matrix)을 2차원 텐서라고 합니다. 2D 텐서라고도 합니다. 텐서의 크기란, 각 축을 따라서 얼마나 많은 차원이 있는지를 나타낸 값입니다. 텐서의 크기를 바로 머릿속으로 떠올릴 수 있으면 모델 설계 시에 유용합니다.
3차원 텐서(다차원 배열)
d = np.array([
[[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [10, 11, 12, 13, 14]],
[[15, 16, 17, 18, 19], [19, 20, 21, 22, 23], [23, 24, 25, 26, 27]]
])
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)
# 텐서의 차원 : 3
# 텐서의 크기(shape) : (2, 3, 5)0차원 ~ 2차원 텐서는 각각 스칼라, 벡터, 행렬이라고 해도 무방하므로 3차원 이상의 텐서부터 본격적으로 텐서라고 부릅니다. 데이터 사이언스 분야 한정으로 주로 3차원 이상의 배열을 텐서라고 부른다고 이해해도 좋습니다. 이 3차원 텐서의 구조를 이해하지 않으면, 복잡한 인공 신경망의 입, 출력값을 이해하는 것이 쉽지 않습니다. 개념 자체는 어렵지 않지만 반드시 알아야하는 개념입니다.
3차원 텐서를 활용한 예제는 나중에 RNN을 배울텐데 그걸 이용해 대략적으로 알려드리면 아래와 같습니다.
- 문서1 → I like NLP
- 문서2 → I like DL
- 문서3 → DL is AI
3차원 텐서 예제
| 단어 | One-hot vector |
| I | [1 0 0 0 0 0] |
| like | [0 1 0 0 0 0] |
| NLP | [0 0 1 0 0 0] |
| DL | [0 0 0 1 0 0] |
| is | [0 0 0 0 1 0] |
| AI | [0 0 0 0 0 1] |
[[[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0]],
[[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0]],
[[0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1]]]컴퓨터는 이진수로 처리가능하기 때문에 이렇게 문자로 주어지면 모릅니다. 그리고 각 단어가 어떤 유사성을 가지고 있는지도 모르지만 이거를 원-핫 벡터를 이용해 벡터로 표현하면 위와 같고 (3,3,6)의 크기를 가지는 3D 텐서가 만들어집니다.
📝벡터 덧셈과 뺄셈
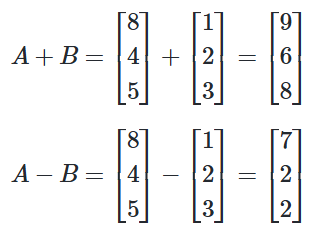
A = np.array([8, 4, 5])
B = np.array([1, 2, 3])
print('두 벡터의 합 :',A+B)
print('두 벡터의 차 :',A-B)
# 두 벡터의 합 : [9 6 8]
# 두 벡터의 차 : [7 2 2]
📝행렬 덧셈과 뺄셈
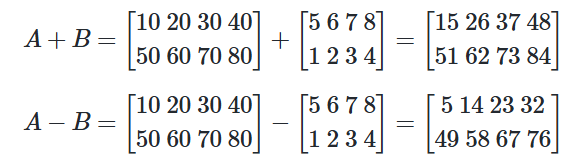
A = np.array([[10, 20, 30, 40], [50, 60, 70, 80]])
B = np.array([[5, 6, 7, 8],[1, 2, 3, 4]])
print('두 행렬의 합 :')
print(A + B)
print('두 행렬의 차 :')
print(A - B)
# 두 행렬의 합 :
# [[15 26 37 48]
# [51 62 73 84]]
# 두 행렬의 차 :
# [[ 5 14 23 32]
# [49 58 67 76]]
📝벡터의 내적
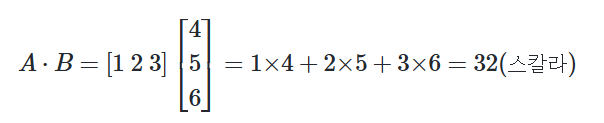
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])
print('두 벡터의 내적 :',np.dot(A, B))
# 두 벡터의 내적 : 32
📝행렬의 곱셈
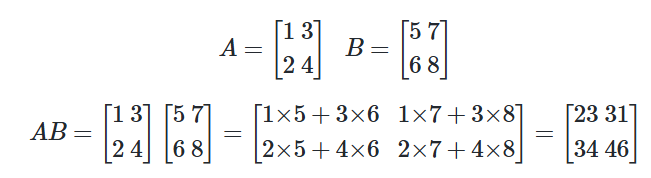
A = np.array([[1, 3],[2, 4]])
B = np.array([[5, 7],[6, 8]])
print('두 행렬의 행렬곱 :')
print(np.matmul(A, B))
# 두 행렬의 행렬곱 :
# [[23 31]
# [34 46]]
📝다중선형 회귀 행렬 연산으로 이해하기
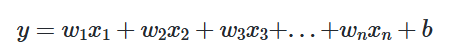
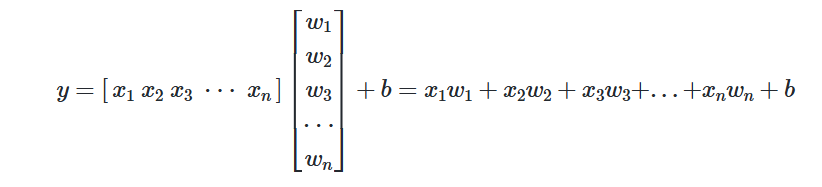
다중 선형 회귀식을 행렬로 표현이 가능하다. 왜 이렇게 할까?
- 기본적으로 가독성이 좋아진다.
- 벡터화된 계산은 컴퓨터가 빨리 처리할 수 있습니다.
- 반복문 없이 한줄로 처리가 가능합니다.
# 내적 사용
import numpy as np
x = np.array([1.2, 0.7, 3.1])
w = np.array([0.5, 2.1, -1.3])
b = 0.2
y = np.dot(w, x) + b
# 내적 사용하지 않은 코드 (반복문)
x = [1.2, 0.7, 3.1]
w = [0.5, 2.1, -1.3]
b = 0.2
y = 0
for i in range(len(x)):
y += w[i] * x[i]
y += b
행렬 연산 예제
| size(feet2)(x1) | number of bedrooms(x2) | number of floors(x3) | age of home(x4) | price($1000)(y) |
| 1800 | 2 | 1 | 10 | 207 |
| 1200 | 4 | 2 | 20 | 176 |
| 1700 | 3 | 2 | 15 | 213 |
| 1500 | 5 | 1 | 10 | 234 |
| 1100 | 2 | 2 | 10 | 155 |
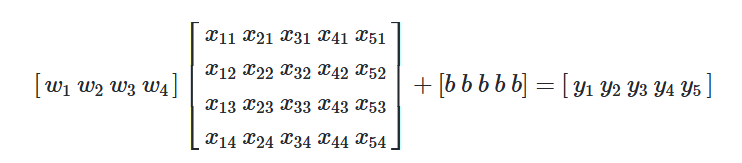
가중치와 입력값을 곱하고 절편값 b를 더해 원하는 결과를 얻어낼 수 있습니다.
📝다중 클래스 분류(Multi-class Classification)
이진 분류가 두 개의 선택지 중 하나를 고르는 문제였다면, 세 개 이상의 선택지 중 하나를 고르는 문제를 다중 클래스 분류라고 합니다. 아래의 붓꽃 품종 예측 데이터는 꽃받침 길이, 꽃받침 넓이, 꽃잎 길이, 꽃잎 넓이로부터 setosa, versicolor, virginica라는 3개의 품종 중 어떤 품종인지를 예측하는 문제를 위한 데이터로 전형적인 다중 클래스 분류 문제를 위한 데이터입니다.
📝소프트맥스 함수(Softmax function)
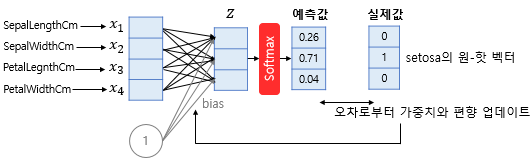
소프트맥스 함수는 선택해야 하는 선택지의 총 개수를 k라고 할 때, k차원의 벡터를 입력받아 각 클래스에 대한 확률을 추정합니다. 꽃에 대한 분류를 할 때 4가지의 입력값을 받고 각 꽃의 특징에 따른 가중치를 받으며 Softmax함수를 거치면 그걸 0~1사이에 값으로 변환시켜줍니다. 오차로 인한 가중치화 편향을 업데이트하며 꽃에 해당하는 원-핫 벡터로 변경합니다.
문제 사항이 두가지가 있습니다.
- 변수는 4개지만 예측 클래스는 3개인 경우 차원을 축소시켜야합니다.
- 예측값으로부터 실제값에 대한 오차를 수정해서 실제값하고 동일하게 만들어야합니다.
1) 차원축소
x1, x2, x3, x4는 꽃에 대한 입력값이면 Z에 해당하는 건 꽃에 대한 확률값입니다. 예를 들면 Z에 1번째 해당하는 부분은 개나리, 2번째는 장미, 3번째는 진달래 이런것인 거죠 그래서 각 꽃에 해당하는 가중치값이 존재합니다. 이걸 계산식으로 표현하면 아래와 같습니다.
- x1w11 + x2w12 + x3w13+ x4w14 = z1
- x1w21 + x2w22 + x3w23+ x4w24 = z2
- x1w31 + x2w32 + x3w33+ x4w34 = z3
2) 오차 범위수정
실제 원-핫 벡터와 값이 유사하지만 다르기 때문에 맞추는 과정인 가중치와 편향 업데이트 과정을 거칩니다.
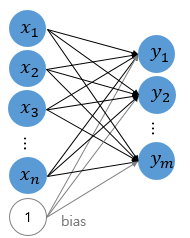
인공 신경망으로 소프트 맥스 함수를 표현하면 위와 같습니다.
📝정수인코딩 vs 원핫인코딩
| 바나나 | 0 |
| 토마토 | 1 |
| 사과 | 2 |
정수 인코딩은 배열의 인덱스 처럼 뭔가 의미 있는 숫자는 아니고 그냥 단지 순서입니다.
| 바나나 | [1,0,0] |
| 토마토 | [0,1,0] |
| 사과 | [0,0,1] |
원-핫 벡터의 경우 각 숫자들이 인덱스처럼 구분만 되는 것이 아니라 단어의 방향성을 부여하는 것으로 숫자와 크기가 의미가 있습니다.
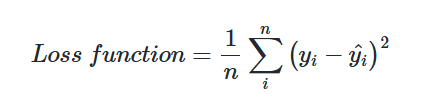
오차 범위 수정을 위해 제곱오차를 이용했을 때 값이 다릅니다
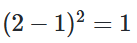
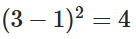
즉, Banana과 Tomato 사이의 오차보다 Banana과 Apple의 오차가 더 큽니다. 이는 기계에게 Banana가 Apple보다는 Tomato에 더 가깝다는 정보를 주는 것과 다름없습니다.
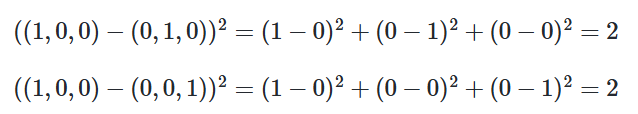
원-핫 벡터를 이용했을 때는 오차범위가 동일하게 책정됩니다.
📝비용 함수(Cost function)
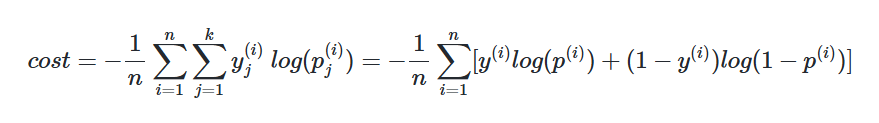
소프트맥스 회귀에서는 비용 함수로 크로스 엔트로피 함수를 사용합니다.
🔗 참고 및 출처