📝인공신경망 처리 과정

인공 신경망은 입력에 대해서 순전파(forward propagation) 연산을 하고, 그리고 순전파 연산을 통해 나온 예측값과 실제값의 오차를 손실 함수(loss function)을 통해 계산하고, 그리고 이 손실(오차)을 미분을 통해서 기울기(gradient)를 구하고, 이를 통해 출력층에서 입력층 방향으로 가중치와 편향을 업데이트 하는 과정인 역전파(back propagation)를 수행합니다.
📝 순전파
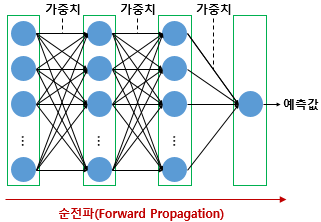
활성화 함수, 은닉층의 수, 각 은닉층의 뉴런 수 등 딥 러닝 모델을 설계하고나면 입력값은 입력층, 은닉층을 지나면서 각 층에서의 가중치와 함께 연산되며 출력층으로 향합니다. 그리고 출력층에서 모든 연산을 마친 예측값이 나오게 됩니다. 이와 같이 입력층에서 출력층 방향으로 예측값의 연산이 진행되는 과정을 순전파라고 합니다.
예제

입력의 차원이 3, 출력의 차원이 2인 위 인공 신경망으로 되어있습니다.

w1~w6 과 b1,b2 총 8개의 매개변수를 가지게 됩니다.
각 입력(특징)은 서로 다른 가중치를 거쳐서 y라는 결과를 만들어지게 됩니다.

이걸 일상생활에 대입하면 코, 입, 얼굴 이라는 3개의 특징을 넣어서 y1인 고양이일 확률 y2인 강아지일 확률에 대해서 출력하는 걸로 정의 할 수 있습니다.

병렬로 처리하면 연산이 빨리 처리 되기 때문에 이런식으로 활용할 수 있습니다.
이렇게 인공 신경망이 다수의 샘플을 동시에 처리하는 것을 우리는 '배치 연산'이라고 부릅니다.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
# 4개의 입력과 8개의 출력
model.add(Dense(8, input_dim=4, activation='relu'))
# 이어서 8개의 출력
model.add(Dense(8, activation='relu'))
# 이어서 3개의 출력
model.add(Dense(3, activation='softmax'))코드로 표현하면 4개의 입력이 있고 렐루를 거쳐서 비선형을 만들며 8개의 출력을 가지게 됩니다.
📝 역전파


순전파를 통해서 나온 결과가 마음에 안 들 때 결과를 재조정하기 위해서 가중치와 절편을 업데이트해야하는데 그 과정을 역전파라고합니다.
📝 손실함수
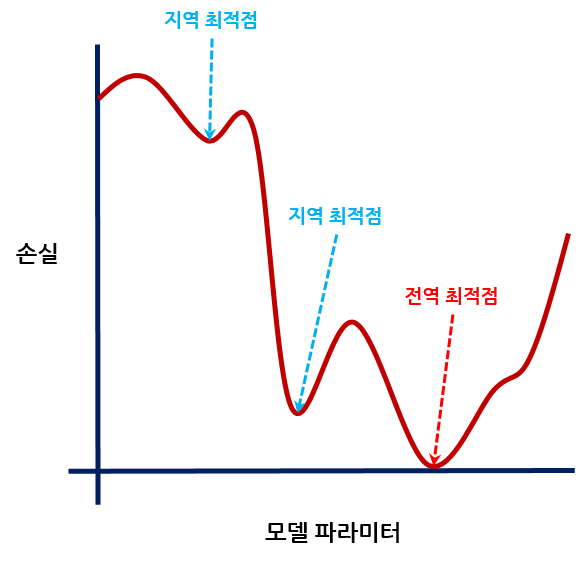
역전파에 사용되며 실제값하고 예측값하고의 차이를 알아내기 위해 손실함수를 이용합니다.
가중치 하나당 손실함수를 통해 나오는 손실값이 1개이고 역전파를 거치며 가중치 수정하면서 그래프 처럼 그리면 위와 같습니다. 최적의 가중치는 손실값이 작은 값이여야하기 때문에 이걸 찾아내기 위해 여러번 반복(역전파)합니다.
| 문제 유형 | 출력층 형태 | 활성화 함수 | 손실 함수 |
| 회귀 (Regression) | 1개 실수값 | 없음 또는 선형 | MSE (Mean Squared Error) |
| 이진 분류 (Binary Classification) | 1개 확률값 | 시그모이드(sigmoid) | Binary Cross-Entropy |
| 다중 클래스 분류 (Multiclass Classification) | 클래스 수만큼 | 소프트맥스(softmax) | Categorical Cross-Entropy |
| 다중 레이블 분류 (Multi-label) | 각 클래스마다 예/아니오 | 시그모이드(sigmoid) | Binary Cross-Entropy (각 클래스마다 따로 계산) |
대부분의 손실함수는 정해져있는 편입니다.
📝 옵티마이저 (모멘텀)

손실함수를 통해 가장 최적의 가중치를 구하기 위해 반복합니다. 가중치를 변화시켜가며 손실값이 가장 적은 값을 구하는 것입니다. 손실값이 가장 적다는 건 가장 이상적인 것이라 판단합니다.
글로벌 미니멈이 가장 최적의 값이지만 로컬 미니멈의 경우 도달했을 때 이게 최적의 값인줄 알고 탈출하지 못하는 상황에서 관성(모멘텀)을 이용해 로컬 미니멈을 탈출해 더 낮은 미니멈을 찾을 수 있는 효과를 얻을 수 있습니다.
📝 옵티마이저 (아다그라드)
서로 다른 매개변수에 서로 다른 학습률을 적용시킵니다. 변화가 많은 매개변수는 학습률이 작게 설정되며 변화가 적은 매개변수는 학습률을 높게 설정시킵니다.
📝 옵티마이저 (알엠에스프롭)
아다그라드의 경우 학습을 계속 진행한 경우에는 나중에 가서 학습률이 지나치게 떨어지는 단점이 있는데 이를 대체하여 단점을 개선했습니다.
📝 옵티마이저 (아담)
알엠에스프롭과 모멘텀 두가지를 합친 방법으로 방향과 학습률 두 가지를 모두 잡기 위한 방법으로 가장 많이 쓰인다.
📝기울기 소실
역전파 과정에서 입력층으로 갈수록 기울기(Gradient)가 점차적으로 작아지는 현상이 발생할 수 있습니다. 입력층에 가까운 층들에서 가중치들이 업데이트가 제대로 되지 않으면 결국 최적의 모델을 찾을 수 없게 됩니다. 이를 기울기 소실(Gradient Vanishing) 이라고 합니다.
기울기 소실을 완화하는 가장 간단한 방법은 은닉층의 활성화 함수로 시그모이드나 하이퍼볼릭탄젠트 함수 대신에 ReLU나 ReLU의 변형 함수와 같은 Leaky ReLU를 사용하는 것입니다.
- 은닉층에서는 시그모이드 함수를 사용하지 마세요.
- Leaky ReLU를 사용하면 모든 입력값에 대해서 기울기가 0에 수렴하지 않아 죽은 ReLU 문제를 해결합니다.
- 은닉층에서는 ReLU나 Leaky ReLU와 같은 ReLU 함수의 변형들을 사용하세요.

# 시그모이드 함수 그래프를 그리는 코드
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()
시그모이드 함수의 출력값이 0 또는 1에 가까워지면, 그래프의 기울기가 완만해지는 모습을 볼 수 있습니다. 기울기가 완만해지는 구간을 주황색, 그렇지 않은 구간을 초록색으로 칠해보겠습니다.
주황색 구간에서는 미분값이 0에 가까운 아주 작은 값입니다. 초록색 구간에서의 미분값은 최대값이 0.25입니다. 다시 말해 시그모이드 함수를 미분한 값은 적어도 0.25 이하의 값입니다. 시그모이드 함수를 활성화 함수로하는 인공 신경망의 층을 쌓는다면, 가중치와 편향을 업데이트 하는 과정인 역전파 과정에서 0에 가까운 값이 누적해서 곱해지게 되면서, 앞단에는 기울기(미분값)가 잘 전달되지 않게 됩니다. 이러한 현상을 기울기 소실(Vanishing Gradient) 문제라고 합니다.

시그모이드 함수를 사용하는 은닉층의 개수가 다수가 될 경우에는 0에 가까운 기울기가 계속 곱해지면 앞단에서는 거의 기울기를 전파받을 수 없게 됩니다. 다시 말해 매개변수 w가 업데이트 되지 않아 학습이 되지를 않습니다.
📝기울기 폭주
기울기가 점차 커지더니 가중치들이 비정상적으로 큰 값이 되면서 결국 발산되기도 합니다. 이를 기울기 폭주(Gradient Exploding) 라고 합니다.
📝가중치 초기화
입력값에 무작정 가중치를 대입하면서 찾아야하지만 무작정 가중치를 넣다가 기울기 소실이나 폭주가 일어날 수 있다. 이거를 효율적으로 처리하기 위해서 가중치 초기화 방법을 이용한다.
- 세이비어 초기화(Xavier Initialization)
- 이전 층과 다음 층의 뉴런 수를 고려해서, 각 층의 출력값들이 너무 커지거나 작아지지 않도록 초기화합니다.
- 시그모이드(sigmoid), tanh 같은 S자 함수에 잘 맞습니다.
- He 초기화(He initialization)
- ReLU는 음수 다 죽이니까, 이전 층 뉴런 수만 고려해서 더 크게 분산을 준다 → 0으로 죽은 놈들은 어쩔 수 없지만 남아있는 애들에게 가중치를 더 크게 주어서 의미를 살린다는 의미이다.
- ReLU 계열 함수 (ReLU, LeakyReLU 등)에 잘 맞습니다.
📝과적합 막는 방법
데이터 양을 늘리기
데이터 양이 적은 경우 데이터 특정 패턴이나 노이즈까지 쉽게 암기가 되기 때문에 과적합 현상이 발생할 확률이 높습니다.
데이터 양이 적은 경우 의도적 기존 데이터를 변형해 데이터 양을 늘리는 이러한 걸 데이터 증식 또는 증강이라고 합니다. 텍스트 데이터의 경우 번역 후 재 번역을 통해 새로운 데이터를 만들어내는 역번역 등이 있습니다.
모델 복잡도 줄이기
신경망은 복잡도는 은닉층과 매개변수 등으로 결정되는데 해당 신경망의 복잡도를 줄입니다.
가중치 규제 적용
복잡한 모델이 간단한 모델보다 과적합될 가능성이 높습니다. 복잡한 모델의 경우 간단한 방법으로 바꾸는 방법으로는 가중치 규제가 있습니다.
- L1 규제
- 가중치 w들의 절대값 합계를 비용 함수에 추가합니다. L1 노름이라고도 합니다.
- 예를 들면 가중치를 죽여서 어떤 특성은 아예 비활성합니다.
- L2 규제
- 모든 가중치 w들의 제곱합을 비용 함수에 추가합니다. L2 노름이라고도 합니다.
- 예를 들면 가중치를 전체적으로 약하게 줘버립니다.
드롭아웃

드롭아웃은 학습 과정에서 신경망의 일부를 사용하지 않는 방법입니다. 예를 들어 드롭아웃의 비율을 0.5로 한다면 학습 과정마다 랜덤으로 절반의 뉴런을 사용하지 않고, 절반의 뉴런만을 사용합니다. 그러다 테스트 할 때는 전부 켜서 테스트를 합니다. 매번 학습할 때마다 뉴런이 랜덤으로 꺼지고 켜지고 하기 때문에 과적합 방법을 방지합니다.